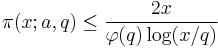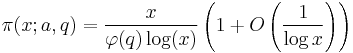Brun–Titchmarsh theorem

In analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression. It states that, if 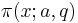$\pi(x;a,q)$ counts the number of primes p congruent to a modulo q with p ≤ x, then

$\pi(x;a,q) \le {2x \over \varphi(q)\log(x/q)}$

for all q < x. The result is proved by sieve methods. By contrast, Dirichlet's theorem on arithmetic progressions gives an asymptotic result, which may be expressed in the form

$\pi(x;a,q) = \frac{x}{\varphi(q)\log(x)} \left({1 %2B O\left(\frac{1}{\log x}\right)}\right)$

but this can only be proved to hold for the more restricted range q < (log x)^c for constant c: this is the Siegel–Walfisz theorem.

References

Hooley, Christopher (1976), Applications of sieve methods to the theory of numbers, Cambridge University Press, p. 10, ISBN 0-521-20915-3
Mikawa, H. (2001), "Brun–Titchmarsh theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=b/b110970
Montgomery, H.L.; Vaughan, R.C. (1973), "The large sieve", Mathematika 20: 119–134 .